Calculo de volúmenes de solidos en revolución - Método de discos y arandelas

 EN ESTA CLASE VIMOS UN TEMA PARECIDO A LOS ANTERIORES, PERO EN LO PERSONAL MENOS COMPLICADO, VIMOS COMO SACAR VOLUMENES HACIENDO GIRAR LOS EJES CON UN FORMULA  NUEVA, ALGO  QUE SE ME COMPLICA SIEMPRE HA SIDO EL ACOMODO DE LOS SIGNOS YA QUE A VECES ME CONFUNDO AL SACAR LOS RESULTADOS

Supón que una función  $\begin{array}{r}𝑓\end{array}$ es continua y no negativa en el intervalo  $\begin{array}{r}[𝑎,𝑏]\end{array}$ , y supón que  $\begin{array}{r}𝑅\end{array}$ es la región entre la curva   $\begin{array}{r}𝑓\end{array}$ y el eje $\begin{array}{r}𝑥\end{array}$ -(Figura 6.3.1a). Si esta región se gira en torno al eje $\begin{array}{r}𝑥\end{array}$ -, generará un sólido que tendrá cortes transversales circulares con radios de  $\begin{array}{r}𝑓(𝑥)\end{array}$  en cada  $\begin{array}{r}𝑥\end{array}$ (Figura 6.3.1b). Cada sección transversal se puede calcular mediante $\begin{array}{r}𝐴(𝑥)=𝜋[𝑓(𝑥){]}^2\end{array}$ .

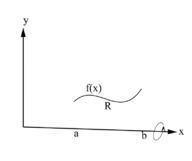
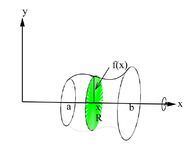
Ya que el volumen se define como $\begin{array}{r}𝑉=\underset{𝑎}{\overset{𝑏}{\int }}𝐴(𝑥)𝑑𝑥\end{array}$ , el volumen del sólido es 

Método de las arandelas

Si la región que se hace girar para generar el sólido de revolución no se acerca al eje de rotación, ni está en él, tendremos que al girarlo sobre el eje se obtendrá un agujero en su centro, es decir, un sólido de revolución con un agujero alrededor del eje de rotación. Si utilizamos el mismo método visto anteriormente para calcular su volumen, en vez de discos, tendremos que las secciones transversales perpendiculares al eje de rotación son arandelas, el área de la arandela está dada como: V = ∫ a b π [ ( f ( x ) ) 2 − ( g ( x ) ) 2 ] d x. 

https://blog.nekomath.com/tag/metodo-de-las-arandelas/

https://flexbooks.ck12.org/cbook/c%C3%A1lculo-2.0/section/6.3/primary/lesson/s%C3%B3lidos-de-revoluci%C3%B3n%3A-vol%C3%BAmenes-por-discos-calc-spn/
CHATGPT

$$A=\pi R^2(x)-\pi r^2(x)=\pi (R^2(x)-r^2(x))<br>$$

$R($

$\begin{array}{r}𝑉=\underset{𝑎}{\overset{𝑏}{\int }}𝜋[𝑓(𝑥){]}^2𝑑𝑥\mathrm{<br>}\end{array}$